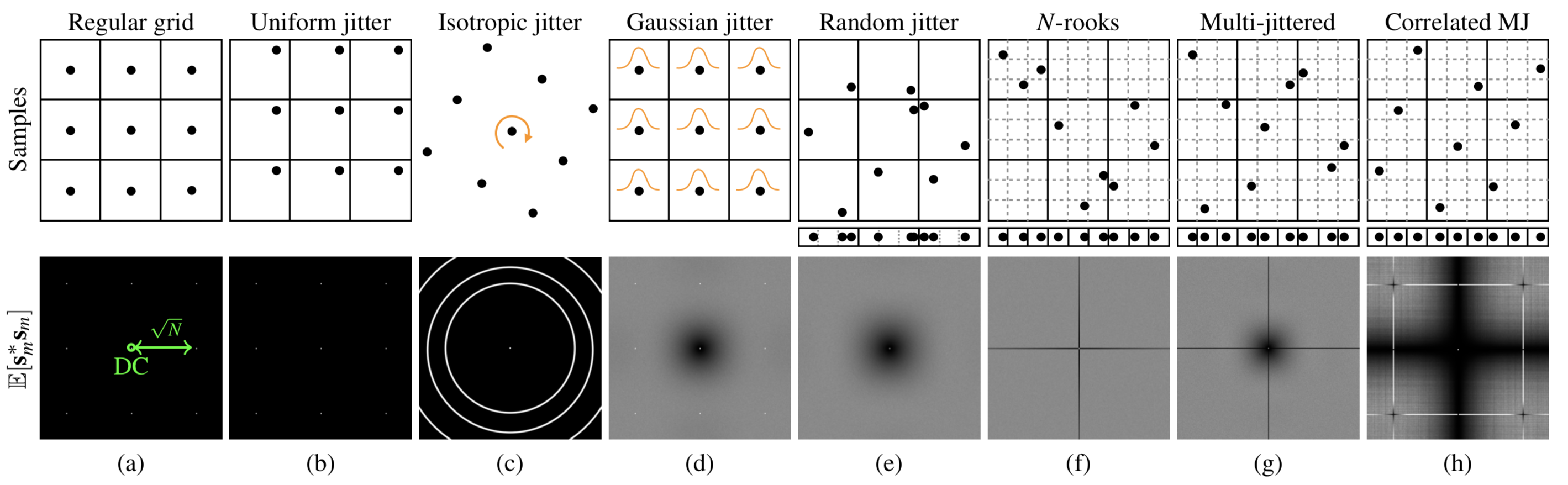

Modern physically based rendering techniques critically depend on approximating integrals of high dimensional functions representing radiant light energy. Monte Carlo based integrators are the choice for complex scenes and effects. These integrators work by sampling the integrand at sample point locations. The distribution of these sample points determines convergence rates and noise in the final renderings. The characteristics of such distributions can be uniquely represented in terms of correlations of sampling point locations. Hence, it is essential to study these correlations to understand and adapt sample distributions for low error in integral approximation. In this work, we aim at providing a comprehensive and accessible overview of the techniques developed over the last decades to analyze such correlations, relate them to error in integrators, and understand when and how to use existing sampling algorithms for effective rendering workflows.
Paper
EG Presentation:
Part 1: Introduction (Gurprit)
PDF
PDF with notes
Keynote
Part 2: Sampling Measures and Error Formulations (Cengiz)
PDF
Powerpoint
Part 3: Error Analysis of Common Sampling Strategies (Gurprit)
PDF
PDF with notes
Keynote
We are grateful to all the anonymous reviewers for their constructive remarks. This work was partially supported by the Fraunhofer and Max Planck cooperation program within the German pact for research and innovation (PFI). Kartic Subr was supported by a Royal Society University Research Fellowship, Ravi Ramamoorthi was supported by NSF grant 1451830 and Wojciech Jarosz was partially supported by NSF grant ISS-1812796.
The Author(s). This is the author's version of the work. It is posted here by permission of The Eurographics Association for your personal use. Not for redistribution. The definitive version is available at diglib.eg.org.